迭代法

迭代法

迭代的一般形式是 \(x_{k+1} = \varphi(x_k)\)。看上去只有 \(\varphi\) 重要，但其实更重要的是隔离区间。

在高等数学中，我们遇到过一些迭代收敛的题目，但这些题目往往总是要考察 \(\mathbb R^+\) 甚至 \(\mathbb R\) 上的收敛性，这使得我们不得不使用单调有界原理、蛛网图等等一系列工具来进行复杂的分析。

但是现在我们的目标是求出解，只要知道迭代过程在一个隔离区间内收敛就好了。所以，选择一个正确的隔离区间是非常、非常、非常关键的。理想的隔离区间应该满足收敛性基本定理：

一般来说只要考察映内性和压缩性。更进一步的，如果目标是求解，那完全可以先行找到不动点，在不动点周围找个小区间说明一下压缩性就好了。这也就是局部收敛定理：

弦截法和迭代法收敛的充分条件

对于给定隔离区间的情况，我们有弦截法和牛顿迭代法收敛的充分条件，它是对函数形态分类讨论后综合得到的：

其中，\(f(a)f(b)<0\) 与 \(f'(x) \ne 0\) 是恰有一单根对应的条件（结合二阶导不变号实际限制了一阶导也不变号）；\(f''(x)\) 不变号是对凸性的要求（不能有拐点），而剩下的 \(f(x_0)f''(x_0) >0\) 的要求则是分类讨论后得到的。对于牛顿迭代法，这个要求没什么歧义，但是对于弦截法，涉及到两个点：

单点弦截法：首先要说明，单点弦截法是一种不动点迭代法，因为 \(x_{k+1}\) 只与 \(x_k\) 有关。所以可以使用收敛性基本定理进行判定，而且一般比较简单。

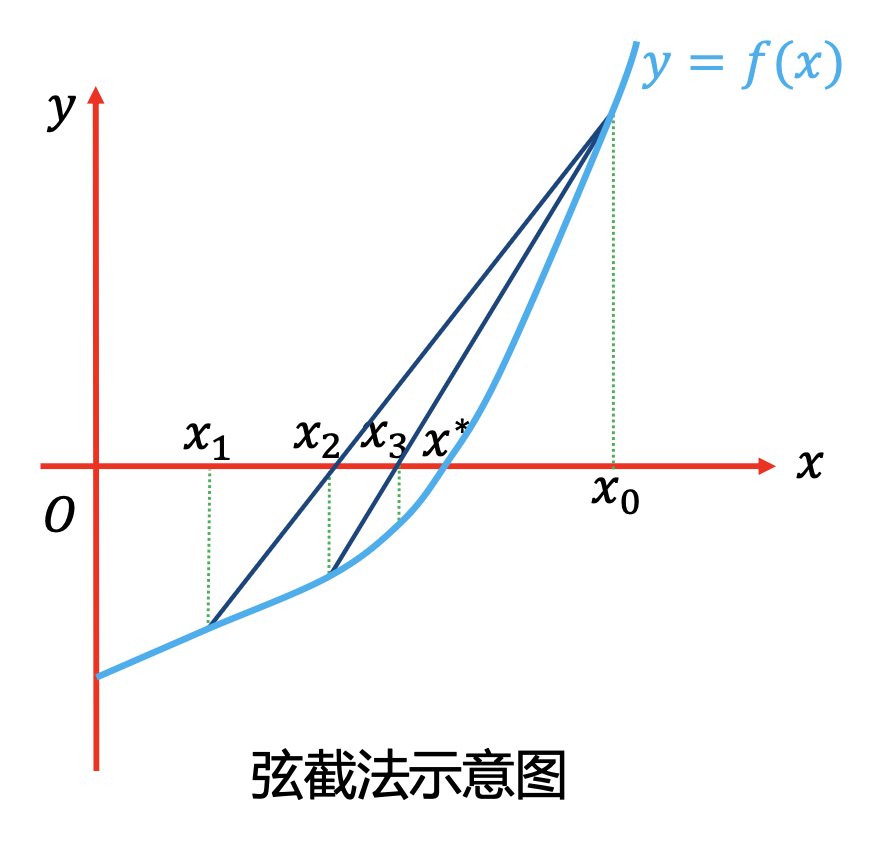
从下面左边的单点弦截法成功示例图可以看出，要确保收敛，单点弦截法要求 \(x_k(k>0)\) 与 \(x_0\) 在根的两侧，或者说 \(f(x_k)f(x_0)<0\)。此时我们只要要求 \(f(x_0)f''(x_0) >0\) 即可。这也很好理解，每一次弦截都是和 \(x_0\) 相关的。

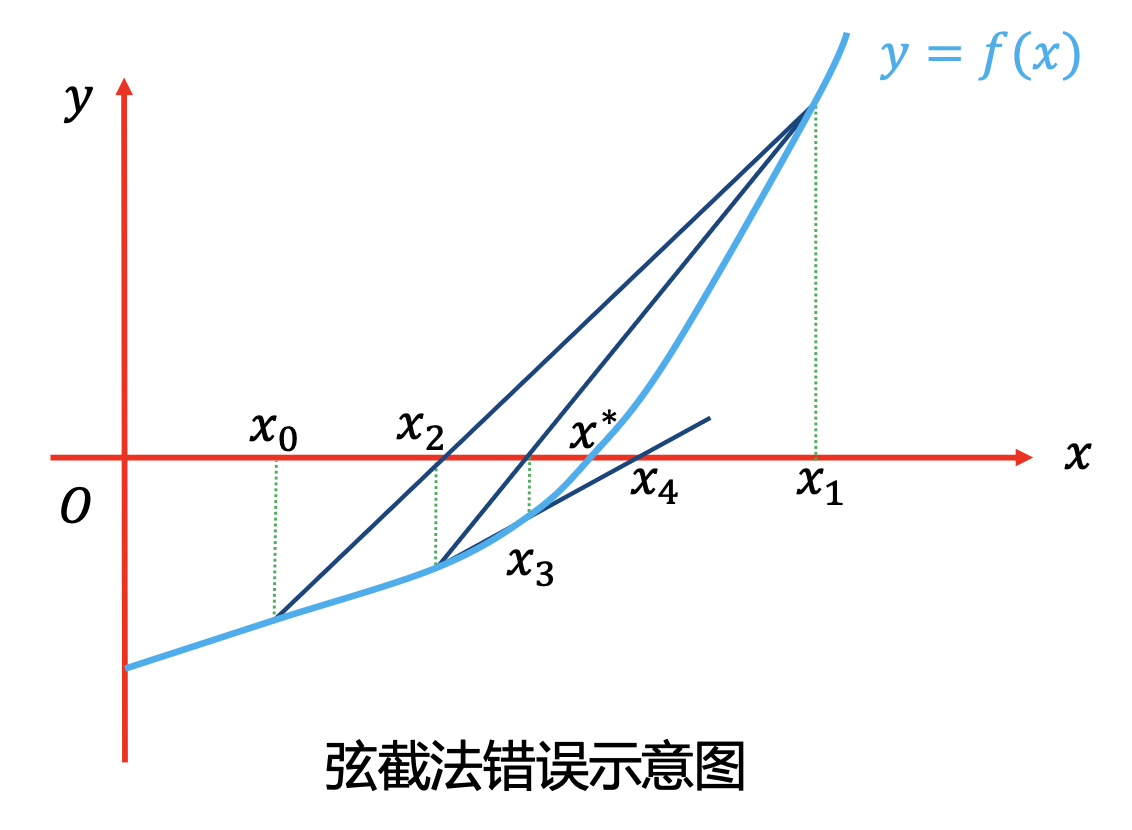
两点弦截法：从上面右边的两点弦截法失败示例图可以看出，如果此时 \(x_0\) 和 \(x_1\) 选择在了根的异侧，那么弦截法就可能失败。所以我们要求 \(f(x_0)f''(x_0)>0\) 的同时，要求 \(f(x_0)f(x_1)>0\)。因为 \(f''(x)\) 始终不变号，所以这也相当于要求 \(f(x_1)f''(x_1)>0\)。

将它与牛顿法类比可以更好的理解这一点：我们实际上在用一阶差商 \(\frac{f(x_k)-f(x_{k-1})}{x_k - x_{k-1}}\) 近似 \(f'(x)\)。根据微分中值定理，在迭代中，可能取到 \(x_0\) 到 \(x_1\) 之间的任何一个 \(\xi\) 的导数信息。为了确保一定收敛，我们希望 \(x_0\) 到 \(x_1\) 内处处都有 \(f(x)f''(x)>0\)。再考虑到二阶导不变号，一阶导不为零的性质，只要要求 \(f(x_0)f''(x_0)>0\) 与 \(f(x_1)f''(x_1)>0\) 就行了。

计算收敛阶数

这是比较简单的高数内容。若：

\[ 0 < \lim_{n\to \infty} \frac{\delta(x_n)}{\delta(x_{n-1})^p} < +\infty \]

称迭代法 \(p\) 阶收敛。这也有一个方便计算的定理，但不背也不影响做题：整数阶超线性收敛定理。